Основная цель расчета электрической цепи заключается в определении токов в её ветвях. Зная токи, несложно отыскать напряжения и мощность веток и отдельных частей цепи. Связь между ЭДС, напряжениями и токами линейных электрических цепей выражается линейными уравнениями. Значения токов, напряжений и мощностей дают возможность оценить условия и эффективность работы электротехнического оборудования во всех участках электрической цепи.
Для расчета электрических цепей с законом Ома используются два закона Кирхгофа.
1-ый закон Кирхгофа
1-ый закон Кирхгофа применяется к узлам электрических цепей:
В ветвях, образующих узел электрической цепи, алгебраическая сумма токов равна нулю:
∑ I = 0.
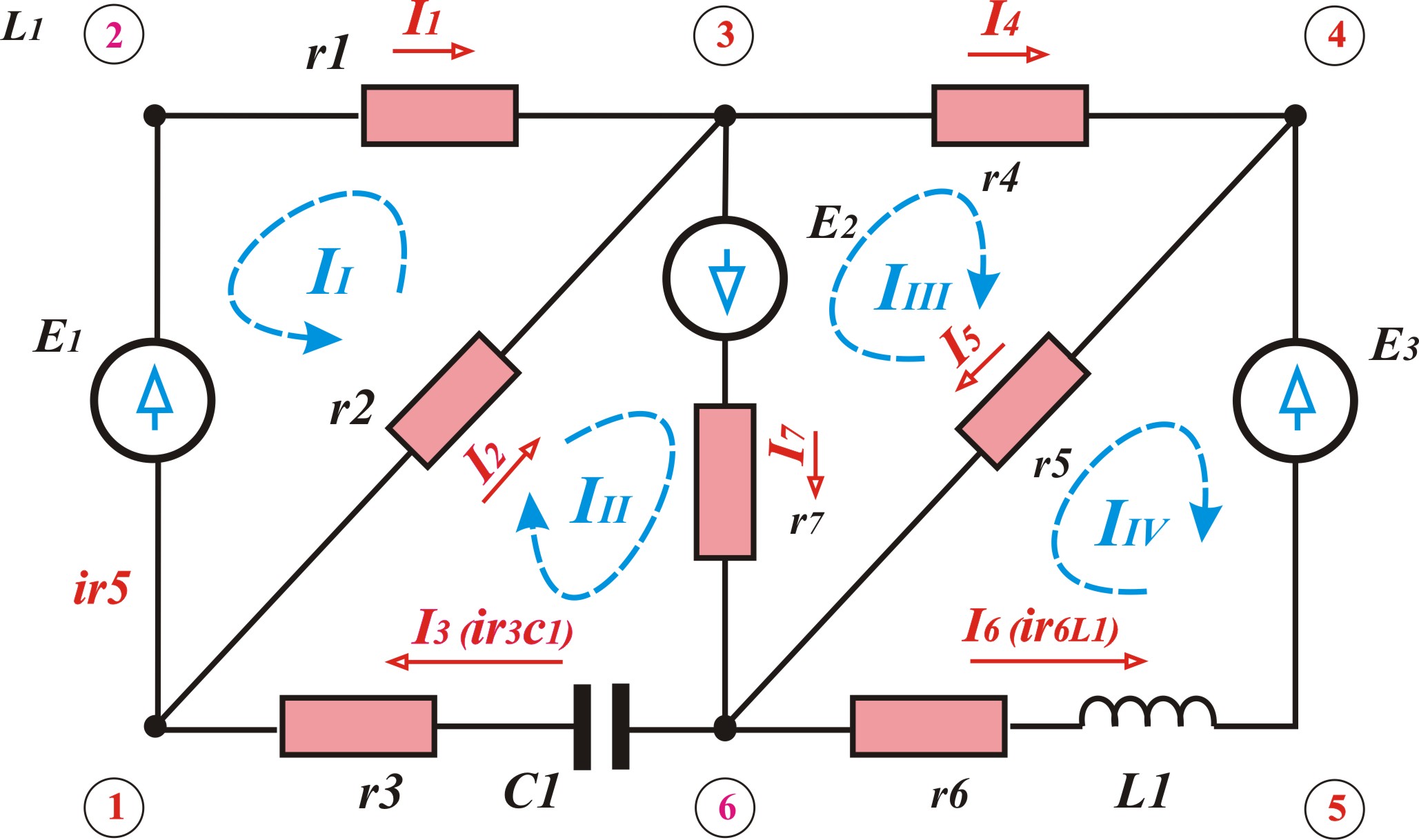
В эту сумму токи входят с различными знаками зависимо от направления их по отношению к узлу. На основание первого закона Кирхгофа для каждого узла можно составить уравнения токов. К примеру, для точки 2 (Рис. 5(в) и (г) ) уравнение имеет вид: (см. ссылку — перейти)
I1 + I6 – I3 = 0
I1 + I6 = I3.
2-ой закон Кирхгофа
2-ой закон Кирхгофа применяется к контурам электрических цепей:
В контуре электрической цепи алгебраическая сумма напряжений на его ветвях равна нулю:
∑ U = 0.
Для подтверждения второго закона Кирхгофа обойдём контур по часовой стрелке (Рис. 6) 1-2-3-4-5-6-1 и запишем потенциалы точек контура по обозначенным фронтам токов в ветвях, которые выбраны произвольно. Обход начнём с точки 1, потенциал которой V1. Потенциал следующей точки выразим относительно предшествующей: V2 = V1 + E1; V3 = V2 – I1; V4 = V3 — I4; V5 = V4 – E3; V6 = V5 + I6; V1 = V6 – I3.
Изменение потенциала по избранному контуру должно быть равно нулю, т.к. оно выражает работу, затраченную на перемещение частиц, владеющих совместно единицей заряда, по замкнутому пути в электрических полях источников и приёмников энергии (см. Рис. 1). Тогда в замкнутом контуре:
V1 + V2 + V3 + V4 + V5 + V6 = 0, E1 – I1 – I4 – E3 + I6 – I3 = 0,
либо — (E1 – I1) + I4 + (E3 – I6) + I2 = 0.
Соответственно в этом уравнении напряжение веток: 3 – 2 – 1 E1 – I1 = U3,1; 4 – 5 – 6 E3 – I6 = U4,6; 3 – 4 I4 = U3,4; 6 – 1 I2 = U6,1,
потому U3,1 + U4,6 + U6,1 = 0. В данном уравнении напряжения числятся положительными (по обходу контура), а направления против обхода – отрицательными.
Перепишем уравнение в следующем виде:
I1 + I4 + I3 – I6 = E1 – E3.
В таком виде уравнение даёт другую формулировку второго закона Кирхгофа:
В контуре электрической цепи алгебраическая сумма падений напряжения в пассивных элементах равна алгебраической сумме ЭДС этого контура:
∑ IR = ∑E.
Соответственно к другим контурам составляются другие уравнению, которые несложно составить, не прибегая к выражениям потенциалов точек контура, пользуясь обычным правилом. В левую часть уравнения записывать алгебраическую сумму падений напряжения в пассивных элементах контура, а в правую алгебраическую сумму ЭДС, встречающихся при обходе контура. Соответственно положительными числятся токи и ЭДС, направление которых совпадает с направлением обхода.
1-ый и 2-ой законы Кирхгофа
Корректнее данные утверждения, которые в заголовке названы первым и вторым законами Кирхгофа было бы именовать правилами Кирхгофа. Данные правила используют при расчетах характеристик сложных разветвленных электрических цепей неизменного тока. Электрические цепи могут содержать огромное количество сопротивлений, источников тока, иметь в собственном составе несколько замкнутых контуров и узлов. Характеристики, характеризующие схожую цепь можно вычислить, если применять отлично известные законы Ома и сохранения заряда. Правила Кирхгофа являются следствиями этих главных законов. Но с помощью правил Кирхгофа можно значимой упростить функцию составления уравнений, которые свяжут силы тока, сопротивления и электродвижущие силы (ЭДС) источников в разветвленной цепи неизменного тока. Существует два правила Кирхгофа для электрических цепей неизменного тока. 1-ое правило Кирхгофа именуют правилом узлов. Оно связывает в одно уравнение токи, сходящиеся в узле. 2-ое правило Кирхгофа относится к замкнутым контурам, которые можно выделить в сложной цепи.
1-ый закон Кирхгофа
В разветвлённой электрической цепи в одной точке могут сходиться более 2-ух проводников, по которым текут токи, такую точку цепи именуют узлом (разветвлением) цепи. Помня, что сила тока является алгебраической величиной, запишем ее сумму в узле с учетом символов:
где N – число токов, которые сходятся в узле. Выражение (1) именуют первым правилом Кирхгофа (правило узлов): сумма токов, текущих через сопротивления в цепи неизменного тока, с учетом их знака, сходящихся в узле, равна нулю.
Символ у тока (плюс либо минус) выбирают произвольно, но при всем этом следует считать, что все входящие в узел токи имеют однообразные знаки, а все исходящие из узла токи имеют обратные входящим, знаки. Допустим, все входящие токи мы примем за положительные, тогда все исходящие их этого узла токи будут отрицательными.
1-ое правило Кирхгофа дает возможность составить независящее уравнение, если в цепи m узлов.
1-ое правило Кирхгофа является следствием закона сохранения заряда.
2-ой закон Кирхгофа
2-ое правило Кирхгофа формулируется для замкнутых контуров, потому его именуют правилом контуров: Суммы произведений алгебраических величин сил тока на наружные и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин посторониих электродвижущих сил (ЭДС) ( ), которые входят в рассматриваемый контур. В математическом виде 2-ой закон Кирхгофа записывают как:
Величины именуют падениями напряжения. До использования второго закона Кирхгофа выбирают положительное направление обхода контура. Это направление берется произвольно, или по часовой стрелке, или против нее. Если направление обхода совпадает с направлением течения тока в рассматриваемом элементе контура, то падение напряжения в формулу второго правила для данного контура заходит со знаком плюс. ЭДС считают положительной, если при движении по контуру (в избранном направлении) первым встречается отрицательный полюс источника. Более верно было бы сказать, что ЭДС считают положительной, если работа посторониих сил по перемещению единичного положительного заряда на рассматриваемом участке цепи в данном направлении обхода контура является положительной величиной.
2-ое правило Кирхгофа — это следствие закона Ома.
Примеры решения задач
Разглядим контур ABCA. За направление обода примем движение по часовой стрелке. Тогда по второму правилу Кирхгофа имеем:
Разглядим контур ACDA. Направление обхода оставим прежним.
Не считая того по закону Ома запишем, что:
Мы получили систему из 4 уравнений:
![\[\left\{ \begin{array}{c} I_1=I_V+I_{2} \\ -I_1R_1-I_VR_V=\varepsilon \\ I_VR_V-I_2R_2-I_2R_3=0 \\ I_V=\frac{U_V}{R_V} \end{array} \qquad (1.5)\]](/wp-content/uploads/2024/03/uravnenie-1-i-2-zakona-kirhgofa_5.png)
Решая данную систему получаем:
![\[\left|\varepsilon \right|=\frac{U_V(R_1R_V+R_1R_2+R_2R_V+R_1R_3+R_3R_V)}{R_{V}(R_2+R_3)}\]](/wp-content/uploads/2024/03/uravnenie-1-i-2-zakona-kirhgofa_6.png){kind=small}
| Задание | Чему равны силы тока, которые текут через резисторы в первом примере? |
| Решение | Воспользуемся системой уравнений, которые получены в примере 1: |
![\[\left\{ \begin{array}{c} I_1=I_V+I_{2} \\ -I_1R_1-I_VR_V=\varepsilon \\ I_VR_V-I_2R_2-I_2R_3=0 \\ I_V=\frac{U_V}{R_V} \end{array} \qquad (2.1)\]](/wp-content/uploads/2024/03/uravnenie-1-i-2-zakona-kirhgofa_7.png)
Из третьего уравнения системы выразим ток , используем уравнения четыре из той же системы, получим:
![\[I_VR_V-I_2R_2-I_2R_3=0\to I_VR_V=\left(R_2+R_3\right)\to I_2=\frac{I_VR_V}{R_2+R_3}=\]](/wp-content/uploads/2024/03/uravnenie-1-i-2-zakona-kirhgofa_8.png){kind=small}
![\[=\frac{U_V}{R_V}\cdot \frac{R_V}{R_2+R_3}=\frac{U_V}{R_2+R_3} \qquad (2.2)\]](/wp-content/uploads/2024/03/uravnenie-1-i-2-zakona-kirhgofa_9.png){kind=small}
Силы тока, текущие через сопротивления и одинаковы и равны . Силу тока. которая течет через сопротивление найдем используя уравнения 1-ое и 4-ое из системы уравнений (2.1) и полученную силу тока :
Законы Кирхгофа они же Правила Кирхгофа для тока и напряжения.
Законы Кирхгофа они же Правила Кирхгофа для тока и напряжения. Kirchhoff current (либо "first") rule (либо "law") & Kirchhohh loop (либо "mesh", либо "second") rule (либо "law") .
- узлы— точки соединения трёх и поболее проводников
- контуры — ЗАМКНУТЫЕ пути из проводников. При всем этом каждый проводник может заходить в несколько контуров.
- ветки — последовательное соединение частей между 2-мя наиблежайшими узлами
Закон токов Кирхгофа
(Правило токов Кирхгофа, ЗТК, ПТК, 1-ый закон Кирхгофа, 1-ое правило Кирхгофа ).
Закон напряжений Кирхгофа
(Правило напряжений Кирхгофа, ЗНК, ПТК, 2-ой закон Кирхгофа, 2-ое правило Кирхгофа).
Алгебраическая сумма токов в хоть какой точке хоть какой цепи равна нулю (значения вытекающих токов берутся с оборотным знаком)
Другими словами, сколько тока втекает в точку цепи ( на практике применяют узел — см. выше), столько из нее и вытекает (из узла и вытекает).
Сколько дает уравнений: Если цепь содержит p узлов, то она описывается p-1 независящими уравнениями токов относительно узлов.
Комфортно считать входящие токи положительными, а выходящие отрицательными.
Алгебраическая сумма падений напряжений по хоть какому ЗАМКНУТОМУ контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю. (Если направление тока совпадает с направлением обхода контура, перепад напряжения считается положительным, в неприятном случае — отрицательным). если в замкнутом контуре k штук ЭДС и n проводников , то:
Другими словами, при обходе цепи по контуру, потенциал, изменяясь, ворачивается к начальному значению.
Сколько дает уравнений: Если цепь содержит n веток, из которых k содержат источники тока (ЭДС) и p узлов , то она описывается n-k-(p-1) независящими уравнениями напряжений относительно узлов. ( т.е. на практике в расчетах опираются на узлы, а не на что попало)
- положительные направления токов в ветвях и обозначить их на схеме (как наверху справа — но там некорректно выделены ветки и узлы. — специально таковой пример приводим);
- положительные направления обхода контуров для составления уравнений по второму закону (с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми, к примеру, по часовой стрелке)
- Если Вы не угадали с рисунком — получите в ответе отрицательные величнины токов и напряжений и всего-то.
Пример: попробуем записать все вероятные уравнения следуя Правилам Кирхгофа для данного рисунка ( он-же — наверху справа, не удивляйтесь) :
Заметим, что он содержит p=3 узла не 6!, k=0 ЭДС, и n=4 ветки (в замкнутых контурах). Ожидаем, поэтому:
- p-1 = 2 уравнения тока
- n-k-(p-1) = 2 уравнения напряжения
- итого ожидаем 4 независящих уравнения
Все другие умные равенства такие как I3=I5, U4=U3+U5 и т.д., которые можно получить из анализа рисунки, строго говоря, не опираются на Правила Кирхгофа, а опираются на здравый смысл и законы Ома. Расчеты по правилам Кирхгофа ведут конкретно по узлам ("относительно узлов"), выделив их за ранее на схеме. Естественно:
- не забываем Главные электротехнические формулы. Мощность. Сопротивление. Ток. Напряжение. Закон Ома.
- помним, что все суждения Правил Кирхгофа относятся как к реальным, так и всеохватывающим ЭДС и падениям напряжения.
Законы Кирхгофа являются производной от глобальных "законов сохранения". Потому: вот очередное принципиальное суждение для инженеров:
- в случаях переноса массы (воды, газа) по трубам массовый расход (а для несжимаемых жидкостей в отсутствии хим реакций и большой расход) является полным аналогом тока и подчиняется Первому Правилу (сколько втекает, столько вытекает).
- аналогом потенциала в таких системах является давление, аналогом ЭДС в таких системах является пререпд давления создаваемый насосами. Аналогом падения напряжения является падение давления. Эти величины подчиняются Второму правилу Кирхгофа ( при обходе трубы по контуру, давление изменяясь ворачивается к начальному значению).
- Единственным принципиальным различием от традиционной электротехники, где сопротивления, в целом, размеренны относительно широких диапазонов тока является тот факт, что гидравлическое сопротивление сильно находится в зависимости от нрава потока, определяемого таковой величиной, как Число Рейнольдса(Re), зависящее от параметров среды и всяких иных черт процесса.
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Дополнительная информация от Инженерного cправочника DPVA, а конкретно — другие подразделы данного раздела:
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не нашли себя в перечне поставщиков, увидели ошибку, либо у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страничку с ошибкой, пожалуйста.
