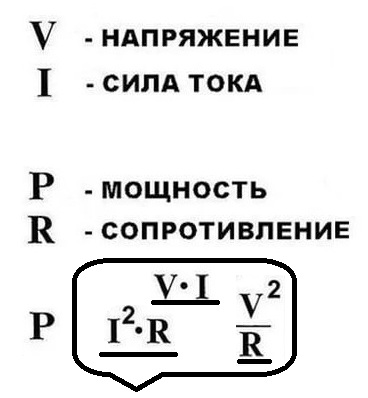
Переменный ток несёт энергию. Потому очень принципиальным является вопрос о мощности в цепи переменного тока.
Пусть и — секундные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени — так малый, что напряжение и ток не успеют за этот период времени сколько-либо поменяться; другими словами, величины и можно считать неизменными в течение интервала .
Пусть за время через наш участок прошёл заряд (в согласовании с правилом выбора знака для силы тока заряд считается положительным, если он переносится в положительном направлении, и отрицательным в неприятном случае). Электрическое поле перемещающихся зарядов совершило при всем этом работу
Мощность тока — это отношение работы электрического поля ко времени, за которое эта работа совершена:
Точно такую же формулу мы получили в своё время для неизменного тока. Но в этом случае мощность находится в зависимости от времени, совершая колебания совместно током и напряжением; потому величина (1) именуется ещё моментальной мощностью.
Из-за наличия сдвига фаз сила тока и напряжение на участке не должны совпадать по знаку (к примеру, может случиться так, что напряжение положительно, а сила тока отрицательна, либо напротив). Соответственно, мощность может быть как положительной, так и отрицательной. Разглядим чуток подробнее оба этих варианта.
1. Мощность положительна: . Напряжение и сила тока имеют однообразные знаки. Это значит, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка увеличивается: она поступает на данный участок из наружной цепи (к примеру, конденсатор заряжается).
2. Мощность отрицательна: . Напряжение и сила тока имеют различные знаки. Стало быть, ток течёт против поля перемещающихся зарядов, образующих этот самый ток.
Как такое может случиться? До боли просто: электрическое поле, возникающее на участке, вроде бы «перевешивает» поле перемещающихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (к примеру, конденсатор разряжается).
Если вы не полностью сообразили, о чём только-только шла речь, не переживайте — далее будут определенные примеры, на которых вы всё и увидите.
Мощность тока через резистор
Пусть переменный ток протекает через резистор сопротивлением . Напряжение на резисторе, как нам понятно, колеблется в фазе с током:
Потому для моментальной мощности получаем:
График зависимости мощности (2) от времени представлен на рис. 1 . Мы лицезреем, что мощность всё время неотрицательна — резистор конфискует энергию из цепи, но не возвращает её назад в цепь.
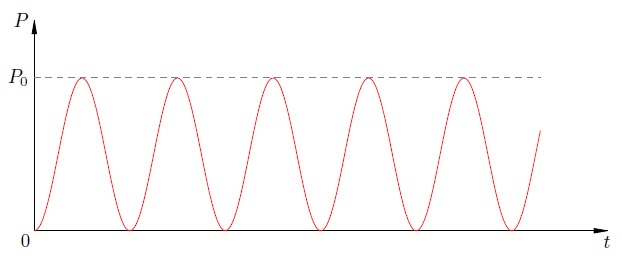
Рис. 1. Мощность переменного тока через резистор
Наибольшее значение нашей мощности связано с амплитудами тока и напряжения обычными формулами:
На практике, но, энтузиазм представляет не наибольшая, а средняя мощность тока. Это и понятно. Возьмите, к примеру, обыденную лампочку, которая пылает у вас дома. По ней течёт ток частотой Гц, т. е. в секунду совершается колебаний силы тока и напряжения. Ясно, что за довольно длительное время на лампочке выделяется некоторая средняя мощность, значение которой находится кое-где между и . Где же конкретно?
Поглядите ещё раз пристально на рис. 1 . Не появляется ли у вас интуитивное чувство, что средняя мощность соответствует «середине» нашей синусоиды и воспринимает потому значение ?
Это чувство совсем верное! Так оно и есть. Очевидно, можно дать математически серьезное определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу гипотезу прямым вычислением, но нам это не надо. Довольно интуитивного осознания обычного и принципиального факта:
среднее значение квадрата синуса (либо косинуса) за период равно .
Данный факт иллюстрируется рисунком 2 .
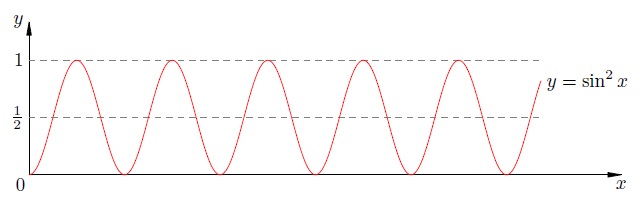
Рис. 2. Среднее значение квадрата синуса равно
Итак, для среднего значения мощности тока на резисторе имеем:
В связи с этими формулами вводятся так именуемые действующие (либо действенные) значения напряжения и силы тока (по сути это есть не что другое, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул безупречного газа (листок «Уравнение состояния безупречного газа»):
Формулы (3) , записанные через действующие значения, стопроцентно подобны подходящим формулам для неизменного тока:
Потому если вы возьмёте лампочку, подключите её поначалу к источнику неизменного напряжения , а потом к источнику переменного напряжения с таким же действующим значением , то в обоих случаях лампочка будет пылать идиентично ярко.
Действующие значения (4) очень важны для практики. Оказывается, вольтметры и амперметры переменного тока демонстрируют конкретно действующие значения (так они устроены). Знайте также, что несчастные вольт из розетки — это действующее значение напряжения бытовой электросети.
Мощность тока через конденсатор
Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на :
Для моментальной мощности получаем:
График зависимости моментальной мощности от времени представлен на рис. 3 .
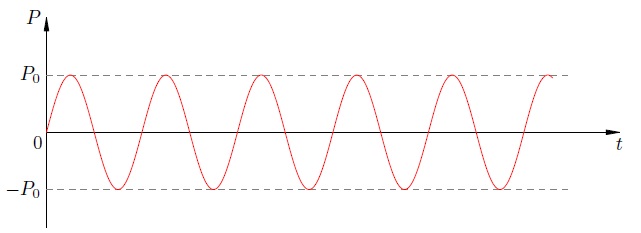
Рис. 3. Мощность переменного тока через конденсатор
Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в этом случае равно нулю! Мы лицезреем это на данный момент как математический факт. Но любопытно было бы с физической точки зрения осознать, почему мощность тока через конденсатор оказывается нулевой.
Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе в протяжении 1-го периода колебаний (рис. 4 ).
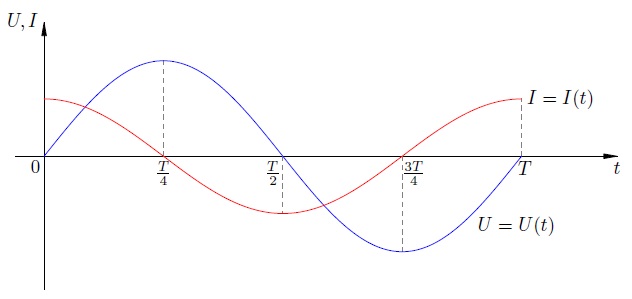
Рис. 4. Напряжение на конденсаторе и сила тока через него
Разглядим последовательно все четыре четверти периода.
1. 1-ая четверть, . Напряжение положительно и увеличивается. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере роста заряда на конденсаторе сила тока убывает.
Моментальная мощность положительна: конденсатор копит энергию, поступающую из наружной цепи. Эта энергия появляется за счёт работы наружного электрического поля, продвигающего заряды на конденсатор.
2. 2-ая четверть, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления наружного электрического поля.В конце 2-ой четверти конденсатор стопроцентно разряжен.
Моментальная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия ворачивается в цепь: она идёт на совершение работы против электрического поля наружной цепи (конденсатор вроде бы «продавливает» заряды в направлении, обратном тому, в каком наружное поле «хочет» их двигать).
3. 3-я четверть, . Наружное электрическое поле меняет направление: напряжение негативно и увеличивается по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.
Ситуация на сто процентов подобна первой четверти, только знаки напряжения и тока — обратные. Мощность положительна: конденсатор вновь копит энергию.
4. Четвёртая четверть, . Напряжение негативно и убывает по модулю. Конденсатор разряжается против наружного поля: сила тока положительна.
Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация подобна 2-ой четверти — опять-таки с подменой подменой символов тока и напряжения на обратные.
Мы лицезреем, что энергия, забранная конденсатором из наружной цепи в процессе первой четверти периода колебаний, вполне ворачивается в цепь в процессе 2-ой четверти. Потом этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.
Мощность тока через катушку
Пусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на :
Для моментальной мощности получаем:
Опять средняя мощность оказывается равной нулю. Предпосылки этого, в общем-то, те же, что и в случае с конденсатором. Разглядим графики напряжения и силы тока через катушку за период (рис. 5 ).
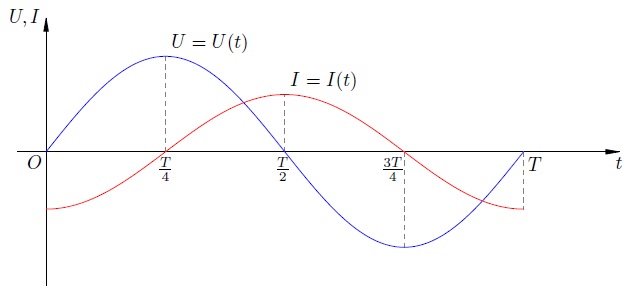
Рис. 5. Напряжение на катушке и сила тока через неё
Мы лицезреем, что в течение 2-ой и четвёртой четвертей периода энергия поступает в катушку из наружной цепи. По правде, напряжение и сила тока имеют однообразные знаки, сила тока увеличивается по модулю; для сотворения тока наружное электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на повышение энергии магнитного поля катушки.
В первой и третьей четвертях периода напряжение и сила тока имеют различные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против наружного электрического поля и совершает тем положительную работу. А за счёт чего совершается эта работа? За счёт энергии, скопленной ранее в катушке.
Таким макаром, энергия, запасаемая в катушке за одну четверть периода, вполне ворачивается в цепь в процессе следующей четверти. Потому средняя мощность, потребляемая катушкой, оказывается равной нулю.
Мощность тока на случайном участке
Сейчас разглядим самый общий случай. Пусть имеется случайный участок цепи — он может содержать резисторы, конденсаторы, катушки. На этот участок подано переменное напряжение .
Как мы знаем из предшествующего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз . Мы записывали это так:
Тогда для моментальной мощности имеем:
Сейчас нам хотелось бы найти, чему равна средняя мощность. Для этого мы преобразуем выражение (5) , используя формулу:
В итоге получим:
Но среднее значение величины равно нулю! Потому средняя мощность оказывается равной:
Данную формулу можно записать при помощи действующих значений (4) напряжения и силы тока:
Формула (7) обхватывает все три рассмотренные выше ситуации. В случае резистора имеем , и мы приходим к формуле (3) . Для конденсатора и катушки , и средняя мощность равна нулю.
Не считая того, формула (7) даёт представление о очень общей дилемме, связанной с передачей электроэнергии. Очень принципиально, дабы у потребителя был как можно поближе к единице. По другому потребитель начнёт возвращать значительную часть энергии вспять в сеть (что ему совершенно нерентабельно), и к тому же возвращаемая энергия будет невозвратно расходоваться на нагревание проводов и других частей цепи.
С этой неувязкой приходится сталкиваться разработчикам электрических схем, содержащих электродвигатели. Обмотки электродвигателей владеют большенными индуктивностями, и появляется ситуация, близкая к «чистой» катушке. Дабы избежать никчемного циркулирования энергии по сети, в цепь включают дополнительные элементы, сдвигающие фазу — к примеру, так именуемые компенсирующие конденсаторы.
Вспоминаем физику: электричество
Электрическая энергия является более распространенным видом энергии и по праву может считаться основой современной цивилизации. Она отыскала обширное использование в быту и во всех отраслях народного хозяйства. Тяжело перечислить все наименования электробытовых устройств: холодильники, стиральные машины, кондюки, вентиляторы, телеки, магнитофоны, осветительные приборы и т.д. Нельзя представить индустрия без электроэнергии. В сельском хозяйстве использование электричества безпрерывно расширяется: кормление и поение животных, уход за ними, отопление и вентиляция, инкубаторы, калориферы, сушилки и т.д.
Электрический ток и его мощность

Современная наука еще не может до конца разъяснить природу электричества. Нам, вобщем, полностью довольно представления о том, что электрический ток — это направленное движение электронов в проводнике. И что этот самый ток может совершать работу, к примеру, крутить электродвигатель, нагревать электроплитку, давать свет. Эта работа является следствием того, что под действием электрического поля происходит перенос, перемещение электронов в проводнике, что тоже значит совершение некоторой работы.
Как вы помните, электрический ток характеризуется 2-мя основными параметрами: напряжением и силой тока.
Напряжение есть разность потенциалов между 2-мя полюсами источника тока при замкнутой электрической цепи.
Сила тока — это количество электричества, проходящего через поперечное сечение цепи в течение одной секунды.
Просто увидеть, что оба термина «напряжение» и «сила тока» не являются первичными, они определяются через другие понятия, в этом случае — «потенциал» и «количество электричества». Но мы опять не будем углубляться в физические теории, ограничившись приведенными определениями, приняв их за первичные. В конце концов, нам принципиально только научиться использовать эти понятия на практике.
Вы, естественно, понимаете еще со школы, напряжение принято обозначать буковкой U и единицей измерения напряжения является вольт (В). Сила тока измеряется в амперах (А) и обозначается латинской буковкой I.
Как уже было сказано в предшествующей статье, способность создавать работу характеризуется величиной, которая именуется энергией. А отношение работы, выполняемой за некоторый промежуток времени, к этому промежутку времени именуется мощностью. Так как ток тоже может совершать работу, понятие мощности применимо и в данном случае.
Мощность неизменного электрического тока обозначается буковкой P и рассчитывается по формуле P=U*I, другими словами является произведением напряжения на силу тока. Другими словами чем больше напряжение и сила тока, тем больше совершается работы в единицу времени, другими словами больше мощность электрического тока. Мы не будем заниматься выяснением того, почему это конкретно так, примем это утверждение на веру (оно обусловлено в физике и вы сможете при желании отыскать это обоснование).
Единицей электрической мощности является ватт (Вт).
Один ватт — это мощность, которую развивает электрический ток величиной в один ампер при напряжении в один вольт.
Более большими единицами мощности являются:
- 1 киловатт (кВт) = 1000 Вт.
- 1 мега ватт (МВт) = 1000 кВт.
Более маленькие единицы:
- 1 милливатт (мвт) = 10 -3 Вт;
- 1 микроватт (мквт) = 10 -6 Вт.
Мощность будет нам встречаться при оценке солнечных батарей, ветро-генераторов и других устройств, способных создавать электрический ток.
Электрическая цепь
Электрическая цепь — совокупа устройств, частей, созданных для протекания электрического тока, электромагнитные процессы в каких могут быть описаны при помощи понятий сила тока и напряжение.
Электрические цепи подразделяют на линейные и нелинейные. Линейные цепи — это такие, которые состоят только из линейных частей — проводников, сопротивлений, конденсаторов, катушек индуктивности без ферромагнитных сердечников. У линейных частей электрическое сопротивление повсевременно и ток находится в прямо пропорциональной зависимости по отношению к напряжению, что выражается известным законом Ома:
Сила тока в участке цепи прямо пропорциональна напряжению и назад пропорциональна электрическому сопротивлению данного участка цепи,
I=U/R.
Это соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и назад пропорциональна сопротивлению проводника. Величину R принято именовать электрическим сопротивлением. В СИ единицей электрического сопротивления проводников служит ом (Ом). Сопротивлением в 1 Ом обладает таковой участок цепи, в каком при напряжении 1 В появляется ток силой 1 А. Проводники, подчиняющиеся закону Ома, именуются линейными.
Необходимо подчеркнуть, что существует много материалов и устройств, не подчиняющихся закону Ома, к примеру, полупроводниковый диодик либо газоразрядная лампа. Даже у железных проводников при довольно огромных токах наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление железных проводников вырастает с ростом температуры. Другими словами большая часть реальных электрических цепей являются нелинейными.
Нелинейные цепи содержат элементы, электрическое сопротивление которых значительно находится в зависимости от тока либо напряжения, в итоге чего ток не находится в прямо пропорциональной зависимости по отношению к напряжению. Зависимость тока от напряжения в нелинейных цепях выражается так именуемой вольт-амперной чертой, получаемой экспериментально и изображаемой некоторым графиком в системе координат «ток-напряжение».
Нелинейные элементы (усилители, генераторы и т.п.) присваивают электрическим цепям характеристики, недосягаемые в линейных цепях (стабилизация напряжения либо тока, усиление неизменного тока и др.).
Мощность переменного тока
Закон Ома в той форме, как он был сформулирован ваше (I=U/R), справедлив только для цепей неизменного тока. Поэтому и формула мощности тока P=I*U, тоже действует только для цепей неизменного тока. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.
Мощность в цепи переменного тока выражается всеохватывающим числом вида P+i*Q. При всем этом его действительная часть именуется активной мощностью, надуманная часть реактивной мощностью.
Активная мощность охарактеризовывает скорость необратимого перевоплощения электроэнергии в другие виды энергии (термическую и электромагнитную). Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока
Единицей измерения активной мощности является по прежнему ватт, а единицей измерения реактивной мощности — вольт-ампер реактивный (VAr, ВАр, вар).
Но практическое значение имеет полная мощность, как величина, описывающая нагрузки, практически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, полосы электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от практически использованной потребителем энергии.
Полная мощность — величина, равная произведению действующих значений повторяющегося электрического тока I в цепи и напряжения U на её зажимах: S=U*I; связана с активной и реактивной мощностями соотношением: S = sqrt [P 2 + Q 2 ], где P — активная мощность, Q — реактивная мощность, sqrt — знак квадратного корня.
Мощность электрического тока

Мощность электрического тока – сущность величина оказываемой на цепь нагрузки. Потому для контроля состояния цепей нужно рассчитывать мощность и осознавать ее природу (которая в особенности сложна для цепей переменного тока).
О работе тока
Под электрическим током понимают движение электронов в проводящей среде, которая со собственной стороны препятствует этому движению. Величина сопротивления находится в зависимости от материала (есть таблицы с данными о проводимости различных веществ), площади сечения и длины проводника. Механизм такой: электроны соударяются с атомами проводников (с узлами решетки в случае жестких тел), теряя кинетическую энергию. Потому электрическим полем, под действие которого происходит движение заряженных частиц, совершается работа по преодолению сопротивления.
Разглядим участок цепи, к которому приложено неизменное напряжение (U). Оно определяется разностью потенциалов:
$U = \phi_1 – \phi_2$
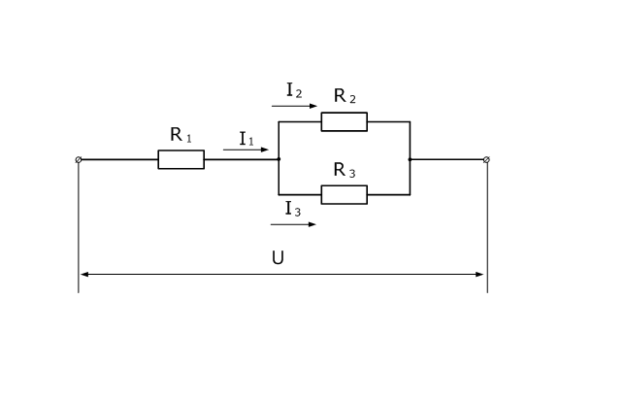
Рис. 1. Участок цепи с напряжением U и сопротивлением R
Напряжение – сущность работа поля по перемещению единичного заряда. Общее же количество заряда – это произведение силы тока на малый промежуток времени dt:
где I – сила тока.
Тогда формула для определения работы тока будет записана следующим образом:
$dA = I \cdot U \cdot dt$
Внимательный читатель увидит, что выражение после знака равенства аналогично выражению, какое содержит закон Джоуля-Ленца. Если поделить правую и левую части на промежуток времени, то получим формулу мощности электрического тока, которая также именуется моментальной:
Что можно записать так:
Как видно, для мощности электрического тока введено особое обозначение – P, но измеряется она, так же, как и механическая мощность N, в ваттах (W – в западной литературе).
При наличии в цепи источника ЭДС, в приведенных формулах U заменяется на $\varepsilon$. Если ЭДС обладает внутренним (своим) сопротивлением, то к общему выражению добавляется мощность, выделяемая на источнике:
где r – внутреннее сопротивление.
Цепи переменного тока
Когда источник тока является переменным (будем считать его однофазовым), в цепи происходит неизменное изменение значения главных величин – I и Q – по синусоидальному закону (но не только лишь). Соответственно, выражения, приобретенные выше для цепей неизменного тока, в данном случае не применимы.
Мощностей переменного тока выделяется три:
Под активной мощностью однофазового синусоидального тока понимают среднее значение мощности за период колебаний:
$P = I \cdot U \cdot cos \phi$, где $\phi$
– разность фаз между током и напряжением, а U и I – среднеквадратичные значения этих величин. Активная мощность измеряется в ваттах. Из-за нее происходит нагрев проводников.
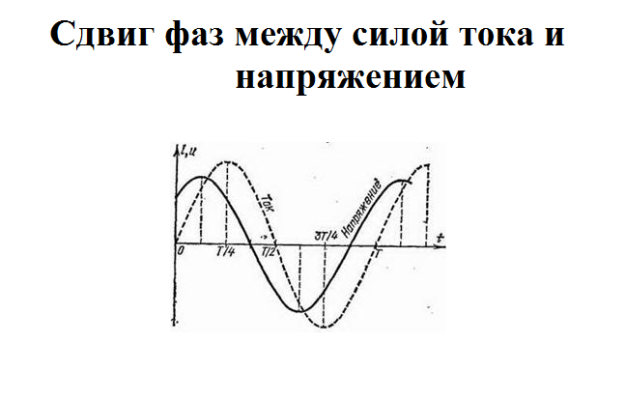
Рис. 2. Сдвиг фаз между силой тока и напряжением.
Под реактивной мощностью понимают нагрузку, которая создается в цепях из-за самих колебаний тока. Она определяется формулой:
$Q = I \cdot U \cdot sin \phi$
Полная мощность определяется действующими значениями напряжения и силы тока.
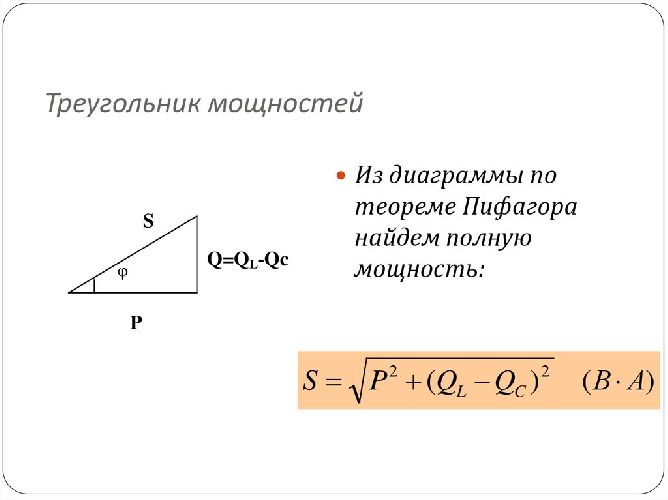
Рис. 3. Треугольник мощностей.
С реактивной и активной мощностями она связана выражением:
Также существует понятие всеохватывающей мощности. Это не отдельный вид мощности, а метод ее вычисления в комплекснозначных величинах, применяемый только для цепей переменного тока.
Задачи
Найти материал проводника, если на нем выделяется мощность 210 Вт. Напряжение – 16 В. Длина проводника – 10 м, площадь сечения – 1 мм 2 .
Решение:
Запишем выражение для мощности:
И для сопротивления:
Сейчас выразим из этих 2-ух формул удельное сопротивление проводника:
Сравнив это значения с табличными значениями удельного сопротивления, узнаем, что проводник сделан из олова.
Что мы узнали?
В процессе урока разглядели вопросы о мощности электрического тока – одной из главных тем электротехники, узнали о различных видах мощности в сетях переменного тока. С целью закрепления пройденного материала приняли решение задачку.