Для расчета различных характеристик электрического тока нередко применяют закон Ома. Но таковой закон не всегда комфортно применять, в особенности в сложных электрических схемах. На замену ему либо в дополнение могут придти другие, к примеру, закон Кирхгофа. В чем заключается отличие, как верно им воспользоваться – все это разглядим ниже.
Формулировка правил
Сходу нужно внести ясность. Хотя в почти всех технических текстах применяется слово закон, по сути это правило. В чем различие? Закон основывается на базовых правдах, фактах, правило несет более абстрактное осознание. Дабы это лучше осознать разглядим базы этого способа.
Из-за трудности вычислений его лучше применять там, где схема имеет узлы и контуры. Узлом именуется место соединения более 2-ух цепей. Это как если взять три и поболее обыденных нити и связать их совместно. Контуром именуется замкнутая цепь, включающая в себя три и поболее таких узла.
Отдельная ветвь может содержать сколько угодно резисторов, под которыми предполагаются нагрузки с активным сопротивлением. Они все соединяются воединыжды в один общий резистор, так как это упрощает решение задачи. Также в цепи может быть один либо несколько источников питания, которые также соединяются воединыжды в один элемент, или их может и не быть. Тогда цепь будет состоять только из сопротивления.
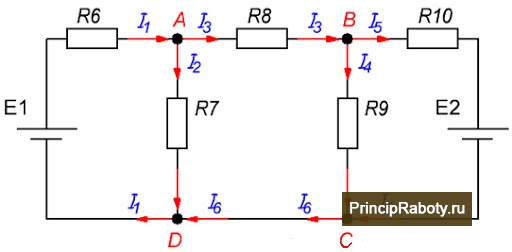
Контур всегда начинается и завершается одним и этим же узлом. Так как узлы обозначаются латинскими либо русскими знаками, то в уравнении будет на одну буковку больше, чем самих соединений. К примеру, участок состоит из узлов A, B, C, D. Тогда обозначение этой петли будет следующим: A, B, C, D, A. По сути, начинать отсчет можно с хоть какой буковкы петли, к примеру, C, D, A, B, C, просто в первом варианте легче будет не запутаться.
Определения
Как уже было сказано ветвь – это отрезок электрической цепи, в какой направление движения заряда происходит в одну сторону. Сходящиеся в узле ветки имеют различное направление токов. Контур может состоять из нескольких внутренних контуров, ветки и узлы которых также относятся к этому контуру. Сам закон Кирхгофа по существу содержит два правила, относящиеся к узлу и контуру. Самым основным и сложным является составление уравнений, учитывающих все составляющие этой формулы.
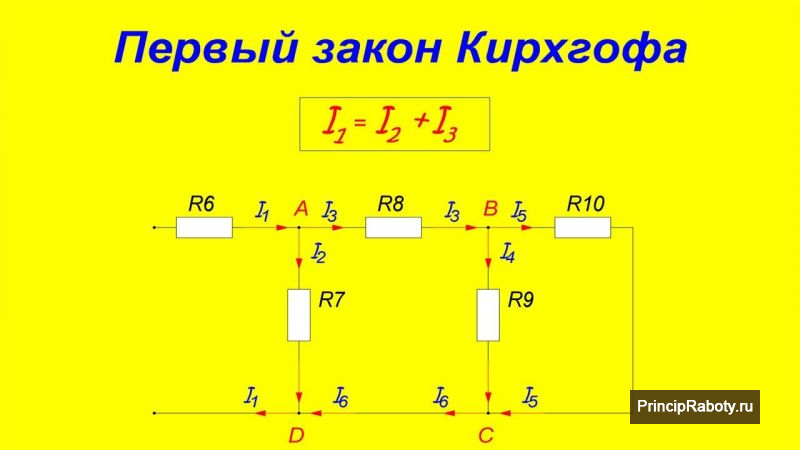
1-ый закон
1-ое правило гласит о сохранении заряда. Согласно ему, в узле напряжение должно быть равно нулю. Это может быть только в этом случае, если все входящие токи в эту точку заходят через одни ветки, а выходят через другие. Соотношение входящих и выходящих токов может быть различным, но суммарная составляющая положительных и отрицательных потенциалов всегда одинакова.
Представим, в узел входят токи по трем веткам, а выходят по двум. Суммарная величина входящих токов будет точно приравниваться суммарной величине выходящих. Если показать это математически, то сумма положительных векторов I1, I2 и I3 будет приравниваться сумме отрицательных векторов I4 и I5.
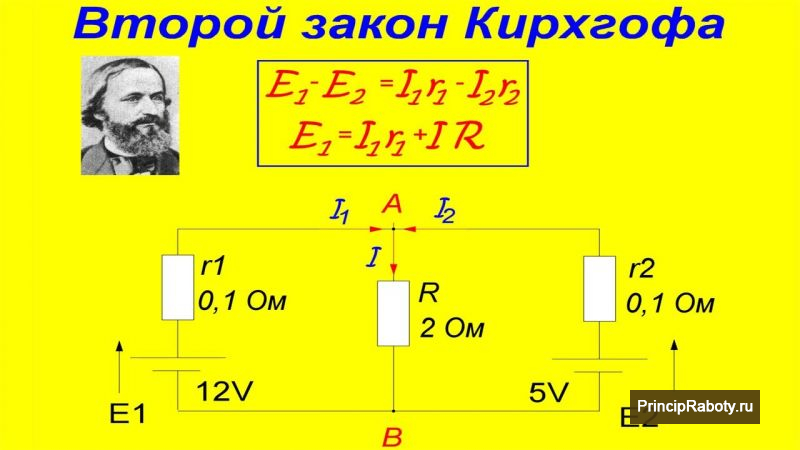
2-ой закон
Это правило связано с сохранением энергии в контуре. Другими словами, энергия источников э. д. с, входящих в контур либо рассматриваемый участок, равна падению напряжения на сопротивлениях этого участка. Если избранный участок не имеет источников питания, то суммарное падение напряжения на всех нагрузках будет равно нулю. До того как перебегать к расчетам, следует ознакомиться еще с некоторыми моментами.
Особенности составления уравнений для расчёта токов и напряжений
Прежде всего выбирается участок, который нужно изучить. Потом на каждой ветке произвольно устанавливается стрелка показывающая направление движения тока. Это необходимо для того, дабы позже не ошибиться. При расчете некорректность направления будет исправлена. Каждую стрелку обозначают буковкой I с индексом. Удобнее будет рассматривать участок, если стрелки находятся в конкретной близости от точки соединения цепей. Источники питания и резисторы тоже обозначают, а у общего резистора добавляют сопротивление.
Снутри участка также произвольно демонстрируют направление обхода, ориентируясь на вероятные потенциалы. Оно нужно для сопоставления направления движения тока. Это сопоставление покажет, какой символ должен стоять у числа. Если оба направления совпадают, ставят символ + и символ – если направления обратны.
Число намеченных целей должно соответствовать количеству избранных неведомых. Допустим, имеется три цепи и нужно вычислить их токи, означает, составленных формул также должно быть три. Выходит, что в новеньком уравнении должен быть хотя бы один новый элемент, которого нет в прошлых задачках.
Значение для электротехники
Правила Кирхгофа являются дополнением к другим законам. Основная сложность состоит в нахождении участков, так как их границы не всегда просто найти. После ограничения подходящей области нужно выделить все неведомые. Составление задач уже относительно легкое дело. Решаются они как обыденные уравнения.
Потому, невзирая на 1-ые трудности, эти правила все таки легче составить и решить, чем применять, допустим, закон Ома. Потому они обширно применяются в электротехнике. Дабы осознать, как на практике применить описанный метод, разглядим один пример.
Значение в арифметике
Имеется контур, состоящий из 4 цепей. В первой содержится источник питания ε1 с внутренним сопротивлением источника r1, во 2-ой какая-то нагрузка R1. 3-я имеет источник питания и нагрузку. 4-ая состоит из нагрузки. Точки B и F являются узлами. Стрелки около них демонстрируют предположительное направление тока. Стрелка снутри участка указывает направление обхода. Нужно отыскать ток в цепях: AK, AB, BF, CD. По идее необходимо составить четыре уравнения, но так как ε1 и R1 единственные на участке KAB, то их объединим в одну цепь. Выходит, необходимо составить три уравнения.
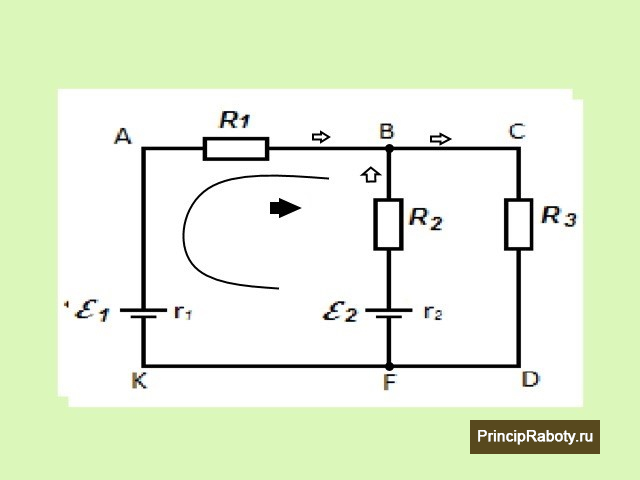
1-ое берется из первого правила: I1 + I2 + I3 = 0. Так как I1, I2 втекают в узел B, они имеют положительный символ, а I3 вытекает из него, то имеет отрицательный символ. Подставляем в уравнение и получаем I1 + I2 — I3 = 0, либо в таком виде I1 + I2 = I3. 2-ое и третье уравнение берем из второго правила. Для этого используем контур BCDFB и преобразуем формулировку в математическое решение: ε2 = I2 × R2 + I3 × R3. Для участка ACDKA получаем соответственно ε1 = I1 × R1 + I3 × R3. Для наглядности вынесем их раздельно.
Вышло три задачи. Определимся с номиналами. 1-ый источник питания равен 6 В, 2-ой – 12 В. Хотя так поступать нельзя, так как параллельные источники питания должны быть одинаковыми, но нам это понадобится для получения принципиального урока. 1-ое сопротивление равно 2 Ом, 2-ое – 4 Ом, третье – 8 Ом.
Осталось воткнуть данные в уравнения и получаем: для второго номера 6 = 2I1 + 8I3, для третьего номера 12 = 4I2 + 8I3. Далее избавляемся от общего неведомого I3. Согласно первому пт, он равен I1 + I2. Подставляем заместо него эту сумму и получаем: 6 = 2I1 + 8(I1 + I2), 12 = 4I2 + 8(I1 + I2). Раскрываем скобки и складываем однообразные неведомые: 6 = 10I1 + 8I2; 12 = 12I2 + 8I1. Дабы отыскать I1, необходимо избавиться от I2. Для этого 1-ое уравнение умножаем на 12, а 2-ое на 8 и получаем: 72 = 120I1 + 96I2; 96 = 96I2 + 64I1. От первого отнимаем 2-ое и записываем остаток -24 = 56I1, либо I1 = -24/56 = -6/14 А. Почему ток отрицательный?
Так как источники питания различные. На втором источнике напряжение выше, чем на первом, потому ток идет в оборотном направлении. Находим I2, для этого значение I1 вставляем в хоть какое из последних уравнений: 96 = 96I2 — 64 24/56. Разделим левую и правую часть на 96 и получим: 1 = I2 — (64×24)/(96×56) либо дробную часть переносим на лево, меняя символ. I2 = 1(64×24)/(96×56), после всех сокращений получаем 1 4/14 А. Для нахождения I3 воспользуемся первым номером: I3 = I1 + I2. I3 = -24/56 + 1 4/14 = 1(4×56)/(14×56) — (24×14)/(56×14) = 1 224/784 -336/784 = 1008/784 -336/784 = 672/774 ≈ 0,87А. Получили I1 = -6/14 А, I2 = 1 4/14 А, I3 ≈ 0,87А.
Закон Кирхгофа в химии
Это правило применимо в химии. Оно гласит, что температура, возникающая при хим реакции, равна изменению теплоемкости, появляющееся при таком действии. Из приведенного выше примера видно, что правила Кирхгофа позволяют с ювелирной точностью определять электрические величины в хоть какой части схемы, какой бы сложной она ни была. Для расчетов нужно только выяснить напряжение и сопротивление на исследуемых цепях.
2-ой закон Кирхгофа
Законы Кирхгофа являются принципиальной частью электротехники, их можно применять для теоретических расчетов и с практической полезностью в случае электрических цепях разветвленного и случайного типа. 1-ый закон и 2-ой закон Кирхгофа пользуются особенным спросом благодаря собственного универсального использования и способности решить различного рода задач. Они работают, так как для линейных цепей, так и для нелинейных, где ток может быть переменным либо неизменным. В некоторых источниках законы Киргофа принято именовать правилами, так как выводы были изготовлены на базе долгого наблюдения за определенными процессами.
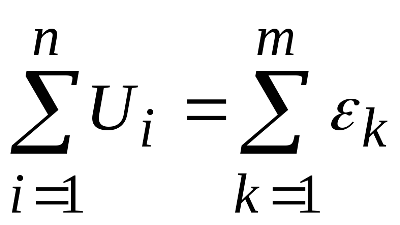
До того как осознать, что собой представляет 2-ой закон Кирхгофа стоит вспомнить, что конкретно говорит 1-ый закон, так как между ними точно должна быть какая-то связь, беря во внимание, в том числе последовательность их возникновения. Невзирая на то какая формулировка, 1-ый закон Кирхгофа говорит одну правду:
1-ая формулировка : Сумма всех токов, которые сводятся в один узел, равна нулю.
2-ая формулировка: Сумма тех токов, которые являются втекающими и вытекающими из одного узла представляет собой одно и то же значение, другими словами эти два значения равны.
Речь конкретно об алгебраической сумме этих токов. Данный закон появился как производное от закона сохранения заряда. Другими словами 1-ый закон показывает на непрерывность тока. 1-ый закон может быть сформулирован по-разному, но вне зависимости от этого он будет означать то же самое понятие. Если 1-ый закон говорит, что сумма всех токов входящие в один узел равна сумме всех токов выходящих из этого узла, то не составит труда сконструировать на базе этого и 2-ое неоспоримое правило Кирхгофа.
Осознание правил Кирхгофа можно упростить, если удостовериться, что такие обыкновенные понятия как ветвь, узел, контур и электрическая цепь являются понятными и доступными. Объяснение можно начать с самого обычного понятия – ветвь, что представляет собой некоторую часть электрической цепи с одинаковым током по всей длине. Узел более сложное понятие, так как он может состоять из определенного количества веток, которые объединены в одной точке. Понятие контур уже некий замкнутый электрический путь, который может состоять из различного количества веток и узлов. Путь непременно закрытый и предполагает возврат в начальную точку после прохождения всех частей электрической цепи. Несколько контуров могут существовать плечо о плечо и разделять между собой свои элементы, так как ветки и узлы. Все эти значения обозначают 2-ой закон Кирхгофа.
2-ой закон Кирхгофа и его определение
В едином замкнутом контуре алгебраическая сумма ЭДС будет приравниваться на значение, которое суммирует конфигурации напряжения на всеобщее количество резистивных частей данного контура.
2-ое правило Кирхгофа животрепещуще в сетях с неизменным и/либо переменным током. В формулировке закона применяется конкретно понятие алгебраическая сумма, так как она может быть указана со знаком плюс либо минус. Четкое определение может быть в таком случае только средством обычного, но действенного метода. Для начала нужно подобрать какое-то направление для обхода контура, по/против часовой стрелке, на собственное усмотрение. Само направление тока подбирается только через элементы цепи. После следует найти знаки «+» и «-» для напряжениях и ЭДС. Напряжения необходимо записывать с отрицательным знаком, когда ток не соответствует обходу контура в плане направления и с плюсом в случае совпадения. То же самое правило необходимо применять и в этом случае, когда стоит отметить ЭДС.
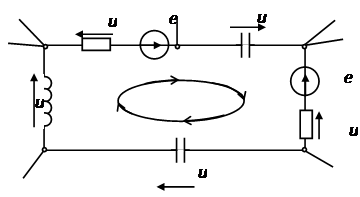
2-ой закон Кирхгофа — практическое использование
На практике 2-ой закон Кирхгофа применяется удачно для расчета электрических цепей. Благодаря его объяснению можно высчитать нужные характеристики в сложных электрических цепях. Когда находится необходимость высчитать значение тока и/либо направление всегда выручит 2-ой закон Кирхгофа. Несмотря на то, что правила Кирхгофа были сформулированы в дальнем 1845 году, они проявили себя как рабочие и не вызывают вопросы ни у кого. Теория электрических цепей была бы неполной без наличия этих законов, которые так отлично подходят для решения разных уравнений в этой области.
Если материал был полезен, вы сможете выслать донат либо поделиться данным материалом в соц сетях:
Законы Кирхгофа — формулы и примеры применения
Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях случайного типа. Законы Кирхгофа имеют особенное значение в электротехнике из-за собственной универсальности, так как применимы для решения всех электротехнических задач. Законы Кирхгофа справедливы для линейных и нелинейных цепей при неизменных и переменных напряжениях и токах.
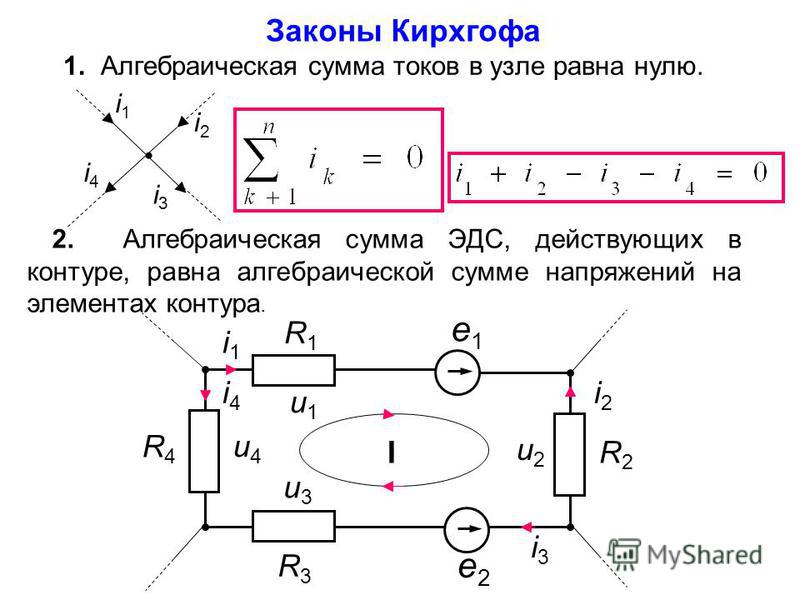
1-ый закон Кирхгофа вытекает из закона сохранения заряда. Он заключается в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.
где – число токов, сходящихся в данном узле. К примеру, для узла электрической цепи (рис. 1) уравнение по первому закону Кирхгофа можно записать в виде I1 — I2 + I3 — I4 + I5 = 0
В этом уравнении токи, направленные к узлу, приняты положительными.
На физическом уровне 1-ый закон Кирхгофа – это закон непрерывности электрического тока.
2-ой закон Кирхгофа: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре
где k – число источников ЭДС; m – число веток в замкнутом контуре; Ii , Ri – ток и сопротивление i -й ветки.
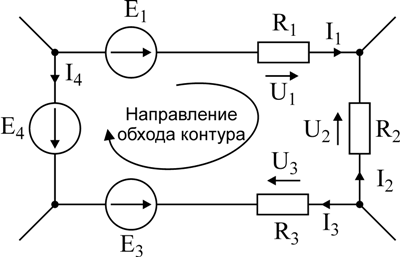
Так, для замкнутого контура схемы (рис. 2 ) Е1 — Е2 + Е3 = I1R1 — I2R2 + I3R3 — I4R4
Замечание о знаках приобретенного уравнения:
1) ЭДС положительна, если ее направление совпадает с направлением произвольно избранного обхода контура;
2) падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода.
На физическом уровне 2-ой закон Кирхгофа охарактеризовывает равновесие напряжений в любом контуре цепи.
Расчет разветвленной электрической цепи при помощи законов Кирхгофа
Способ законов Кирхгофа заключается в решении системы уравнений, составленных по первому и второму законам Кирхгофа.
Способ заключается в составлении уравнений по первому и второму законам Кирхгофа для узлов и контуров электрической цепи и решении этих уравнений с целью определения неведомых токов в ветвях и по ним – напряжений. Потому число неведомых равно числу веток b , поэтому, столько же независящих уравнений нужно составить по первому и второму законам Кирхгофа.
Число уравнений, которые можно составить на основании первого закона, равно числу узлов цепи, при этом только ( y – 1) уравнений являются независящими друг от друга.
Независимость уравнений обеспечивается выбором узлов. Узлы обычно выбирают так, дабы каждый последующий узел отличался от смежных узлов хотя бы одной ветвью. Другие уравнения составляются по второму закону Кирхгофа для независящих контуров, т.е. число уравнений b — (y — 1) = b — y +1 .
Контур именуется независящим, если он содержит хотя бы одну ветвь, не входящую в другие контуры.
Составим систему уравнений Кирхгофа для электрической цепи (рис. 3 ). Схема содержит четыре узла и 6 веток.
Потому по первому закону Кирхгофа составим y — 1 = 4 — 1 = 3 уравнения, а по второму b — y + 1 = 6 — 4 + 1 = 3 , также три уравнения.
Произвольно выберем положительные направления токов во всех ветвях (рис. 4 ). Направление обхода контуров избираем по часовой стрелке.
Составляем нужное число уравнений по первому и второму законам Кирхгофа
Приобретенная система уравнений решается относительно токов. Если при расчете ток в ветки вышел с минусом, то его направление обратно принятому направлению.
Законы Кирхгофа в всеохватывающей форме
Для цепей синусоидального тока законы Кирхгофа формулируются так же, как и для цепей неизменного тока, но только для всеохватывающих значений токов и напряжений.
1-ый закон Кирхгофа: «алгебраическая сумма комплексов тока в узле электрической цепи равна нулю»
2-ой закон Кирхгофа: «в любом замкнутом контуре электрической цепи алгебраическая сумма всеохватывающих ЭДС равна алгебраической сумме всеохватывающих напряжений на всех пассивных элементах этого контура».